The ln() function returns the natural logarithm of a number.
ln(number)
number.ln()
Code language: JavaScript (javascript)The natural logarithm is \(\log_e\), where \(e\) is Euler’s Constant (approximately 2.718281828459045).
For reference, here are the named components of a logarithm:
\(\log_{base} argument = exponent\)A logarithm is the exponent of the base that returns the argument.
Learn more about the natural logarithm:
In plain English, \(log_e\) helps us find out how many periods (i.e. how long) of continuous growth are needed for a starting value to reach a target end value.
\(e\) denotes a continuous rate of growth.
Recall from the article on Euler’s Constant (e), that we can find a starting population’s end number with the following formula:
\(n * e^x\)…where \(n\) is our starting population, and \(x\) is the number of periods.
Let’s say we start out with a population of 1,000, which grows continuously for three years (you can check this answer on WolframAlpha):
\(1000 * e^3 = 20,085\)At the end of three years, our final population is 20,085.
If you want to fully understand why this works, I highly recommend this guide on exponential functions.
Now let’s look at \(log_e\)
Where \(e^x\) tells us how much growth we’ll experience given a number of periods, \(log_ex\) tells us how many periods it’ll take to get a specific end result \(x\).
Here’s the natural logarithm of our earlier result. We’ll take the full result, 20,085, and divide it by the starting population of 1,000 (Check this on WolframAlpha):
\(log_e(20,085/1000) = log_e(20.085) = 3\)We can now see that \(log_ex\) is the inverse of \(e^x\). Therefore, these two are roughly equivalent (20,085 is rounded from the actual result of the first equation):
\(log_e(20.085) = e^3\)This also means:
\(log_ee^3 = 3\)Hopefully this aside has helped to demystify \(log_e\) a bit for you!
Example Formulas
ln(20) /* Output: 2.995732273554 */
e.ln() /* Output: 1 */
Code language: JavaScript (javascript)Example Database
This example database calculates the calculates the number of years needed for a starting population to reach a target end number given a specific growth rate.
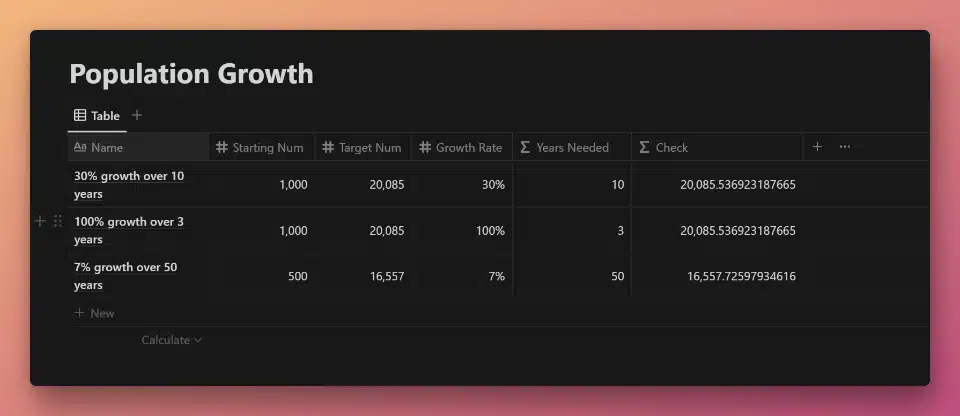
View and Duplicate Database

“Years Needed” Property Formula
round(
ln(
prop("Target Num") /
prop("Starting Num")
) /
prop("Growth Rate")
* 100
) / 100
Code language: JavaScript (javascript)The first part of this formula replicates the mathematical example in the toggle block above.
First, we find the natural logarithm of the quotient of the Target Num and the Starting Num:
\(log_e(Target Num/Starting Num)\)This is done with the following code: ln(prop("Target Num") / prop("Starting Num"))
Next, we divide this result by the Growth Rate.
Finally, the result is passed through the round function, and we use the following trick to round it to two decimal places: round(result * 100)/100
Other formula components used in this example:






