The power (^) operator (also known as the exponentiation operator) allows you to raise a number to a higher power.
number[base] ^ number[exponent]
pow(number[base], number[exponent])
number[base].pow(number[exponent])
Code language: JavaScript (javascript)In technical terms, it raises the first operand to the power of the second operand.
In Notion, the ^ operator has a higher operator precedence than the unaryPlus and unaryMinus operators, and has right-to-left associativity.
You can also use the function version, pow().
Example Formulas
3 ^ 4 /* Output: 81 */
pow(4,3) /* Output: 64 */
4.pow(3) /* Output: 64 */
2 ^ 2 ^ 3 /* Output: 256 - evaluates as 2 ^ (2 ^ 3) */
Code language: JavaScript (javascript)- \(x^0 = 1\)
- \((x^a)^b = x^{ab}\)
- \(x^{a^b} = x^{(a^b)}\) (not all languages respect this, but Notion does)
- \(x^a * y^a = (xy)^a\)
- \(x^a / y^a = (x/y)^a\)
- \(x^a * x^b = x^{a+b}\)
- \(x^a / x^b = x^{a-b}\)
Exponent Associativity
In Notion, the ^ operator has right-to-left associativity, which means that x ^ y ^ z is evaluated as x ^ (y ^ z).
4 ^ 3 ^ 2 == 262,144
4 ^ (3 ^ 2) == 4 ^ 9 == 262,144
(4 ^ 3) ^ 2 == 64 ^ 2 == 4,096
/* Here's that last one according to the (x^a)^b == x^(ab) "Power Rule": */
(4 ^ 3) ^ 2 == 4 ^ (3*2) == 4 ^ 6 = 4,096
Code language: JavaScript (javascript)Not every programming and scripting language uses right-to-left associativity for serial exponentiation. Here’s a write-up comparing the methods for many popular languages. Even though standard mathematical notation has the “Tower Rule”, where \(x^{a^b} = x^{(a^b)}\) (aka: “Work top-down”), the computer science community has not come to a strong consensus on whether x^y^z should be interpreted in the same way.
Example Database
The table below shows exponentiation at work in a Notion database.
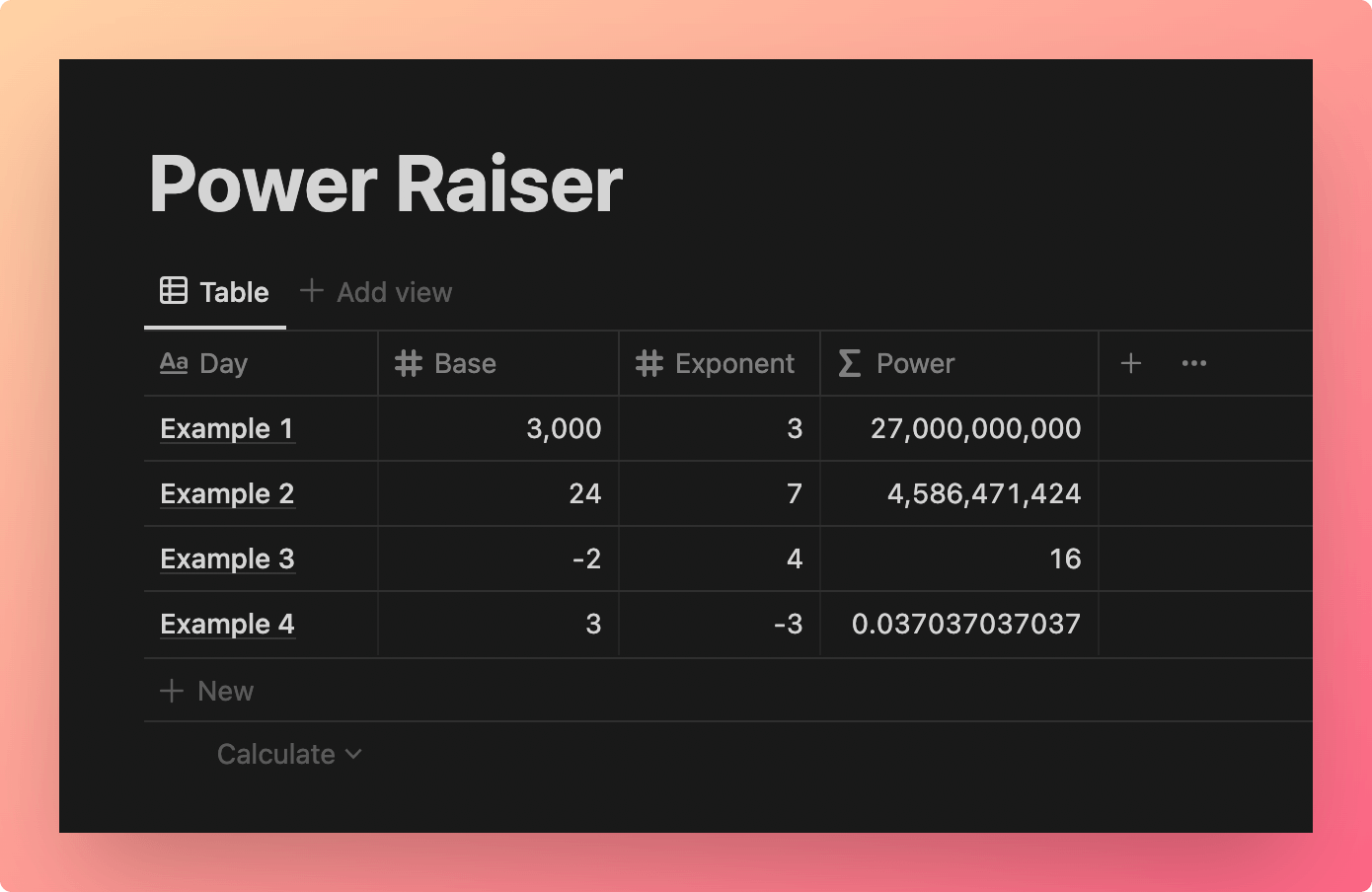
View and Duplicate Database

“Power” Property Formula:
prop("Base") ^ prop("Exponent")
Code language: JavaScript (javascript)Instead of using hard-coded numbers, I’ve called in each property using the prop() function.


