The sqrt() function returns the square root of its argument. sqrt() accepts only numbers.
sqrt(number)
number.sqrt()
Code language: JavaScript (javascript)Example Formulas
sqrt(16) /* Output: 4 */
100.sqrt() /* Output: 10 */
sqrt(73-3^2) /* Output: 8 */
Code language: JavaScript (javascript)Example Database
This example database uses the Pythagorean Theorem to solve for the missing side of any right triangle. Two of the three side lengths must be provided; the Calculator property will solve for the missing one.
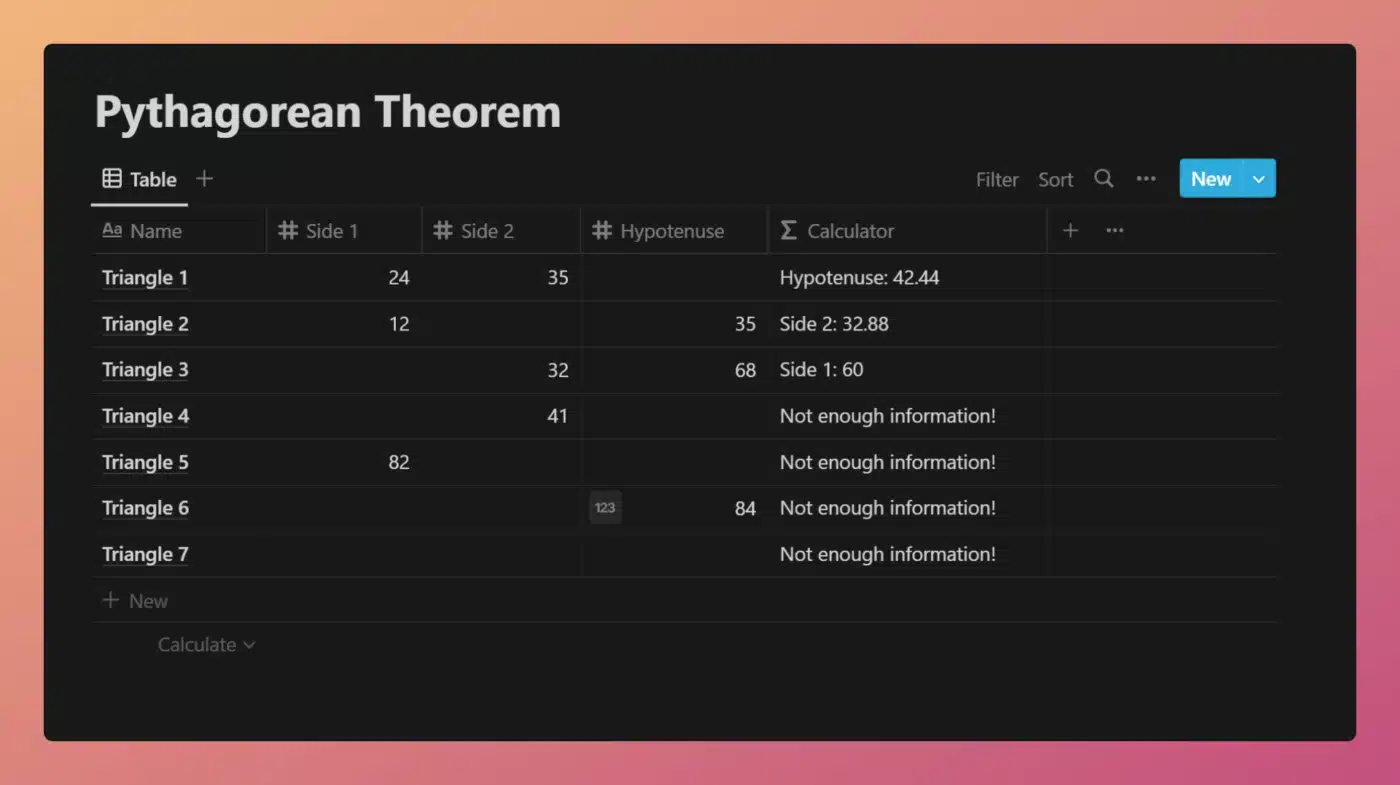
View and Duplicate Database

“Calculator” Property Formula
if(
empty(
prop("Hypotenuse")
) and empty(
prop("Side 1")
) or empty(
prop("Hypotenuse")
) and empty(
prop("Side 2")
) or empty(
prop("Side 1")
) and empty(
prop("Side 2")
),
"Not enough information!",
if(
empty(
prop("Hypotenuse")
),
"Hypotenuse: " +
format(
round(
sqrt(
prop("Side 1")^2 + prop("Side 2")^2
) * 100
) / 100
),
if(
empty(
prop("Side 1")
),
"Side 1: " +
format(
round(
sqrt(
prop("Hypotenuse")^2 -
prop("Side 2")^2
) * 100
) / 100
),
"Side 2: " +
format(
round(
sqrt(
prop("Hypotenuse")^2 -
prop("Side 1")^2
) * 100
) / 100
)
)
)
)
Code language: JavaScript (javascript)I’ll start this explanation off by saying that you can create a much simpler Pythagorean Theorem calculator that solves for the Hypotenuse only with: sqrt(prop("Side 1") ^ 2 + prop("Side 2") ^ 2).
The example above goes a few steps further. It rounds its answer to two decimal places using the round function (see that function’s page for tips on how to round to specific decimal places).
It also solves for any missing side of a right triangle, so long as the other sides have been provided.
The formula first checks to make sure there’s enough information to make a calculation. We use the empty function for this, and we must do so several times since we’re checking to see if any two of the three number properties are empty.
Good to know: The or operator has lower operator precedence than the and operator, so this part of the formula executes as (empty(prop("Hypotenuse")) and empty(prop("Side 1"))) or (empty(prop("Hypotenuse")) and empty(prop("Side 2"))).
In other words, all of the and clauses are executed before the first or clause.
After this error-checking stage, the formula uses a nested if-statement to determine the correct calculation to perform.
If the hypotenuse is missing, we use the following formula to solve for it, where Side 1 and Side 2 are \(a\) and \(b\) respectively:
\(a2+b2\sqrt{a^2+b^2}a2+b2\)If one of the sides is missing, we instead use this formula, where \(c\) is the hypotenuse, and \(b\) is the non-missing side:
\(c2−b2\sqrt{c^2-b^2}c2−b2\)Other formula components used in this example:













