The log2() function returns the base-2 logarithm of a number.
log2(number)
number.log2()
Code language: JavaScript (javascript)For reference, here are the named components of a logarithm:
\(\log_{base} argument = exponent\)A logarithm is the exponent of the base that returns the argument.
Example Formulas
log2(64) /* Output: 6 */
2.log2() /* Output: 1 */
Code language: JavaScript (javascript)Want to learn more about logarithms? Check out this resource:
Computing Logs with Other Bases (Log Base X)
Notion only provides log2(), log10, and ln because those are by far the most commonly-used log bases.
However, if you need to compute a log with a different base, you can use the change of base formula:
\(\log_x y= (\frac{\ln y}{\ln x})\)So, for example:
\(\log_3 81 = (\frac{\ln 81}{\ln 3})\)Here’s a Notion formula to compute this:
ln(81) / ln(3) /* Output: 4 */
Code language: JavaScript (javascript)Example Database
\(log_{2}\) can be used to perform an interesting mathematical trick – finding the length (i.e. number of digits) in any number when represented in binary. It is done by taking the floor value of a number’s \(log_{2}\), then adding one:
\(\lfloor log_{2}n \rfloor + 1\)The example database below shows this trick in action. Unfortunately, actual binary representation of a base-10 number in Notion is not possible (or at least has not been solved by the Notion community), but you can check the result using this converter.
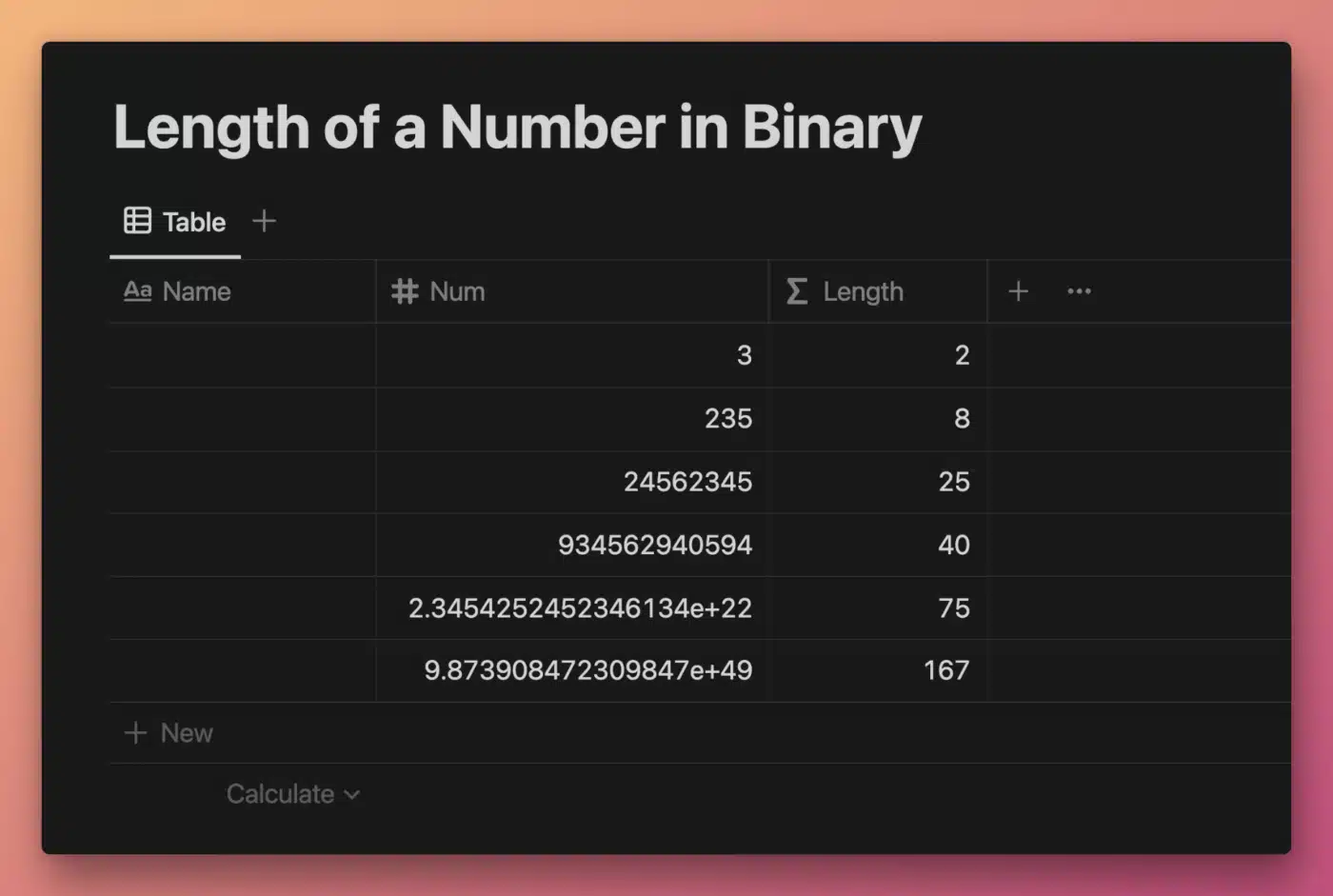
View and Duplicate Database

“Length” Property Formula
prop("Num")
.log2()
.floor()
+ 1
Code language: JavaScript (javascript)If you’re curious about the math behind why this trick works, check out this thread:

The formula itself is quite simple:
- We pass
prop("Num")to thelog10()function. - This value is then run through the floor function in order to round it to its nearest integer of lower or equal value.
- Finally, we add
1.
Other formula components used in this example:






