mod

The remainder (%) operator allows you to get the remainder after dividing the first operand with the second operand.

number % number

mod(number, number)

number.mod(number)
Code language: JavaScript (javascript)

Notion provides a mod() function as well as the % operator (I’ll just reference % for the rest of this article).

Somewhat confusingly, these do not return a true modulus value; they return a remainder (see: Remainder or Modulus? below).

As % and mod() output a remainder, their output values will take the sign (+/-) of the dividend.

For reference, the dividend is the number being divided by the divisor, which produces the quotient:

Example Formulas

19 % 12 /* Output: 7 */

19 mod 12 /* Output: 7 */

mod(-19, 12) /* Output: -7 */

-19.mod(12) /* Output: -7 */
Code language: JavaScript (javascript)

Negative Divisors

As of the Formulas 2.0 update in 2023, if the divisor is negative, both mod() and % will now treat it as a negative integer natively. This is a change from the pre-Formulas 2.0 behavior.

19 % (-12) /* Output: 7 */

/* prop("negative num") == -12 */
19 % prop("negative num") /* Output: 7 */

19 % -12 /* Output: 7 */

mod(19, -12) /* Output: 7 */
Code language: JavaScript (javascript)

Remainder or Modulus?

Just as in JavaScript, Notion’s % operator calculates the remainder of two numbers, not the modulus. Confusingly, the mod() function does this as well, despite its name.

The remainder and modulus of two numbers will be identical when both the dividend and divisor have the same sign (+/-). If their signs differ, however, the modulus will differ from the remainder.

These two articles explain this well:

• Mod and Remainder are Not the Same (Big Machine)
• Remainder operator vs. modulo operator (with JavaScript code) (2Ality)

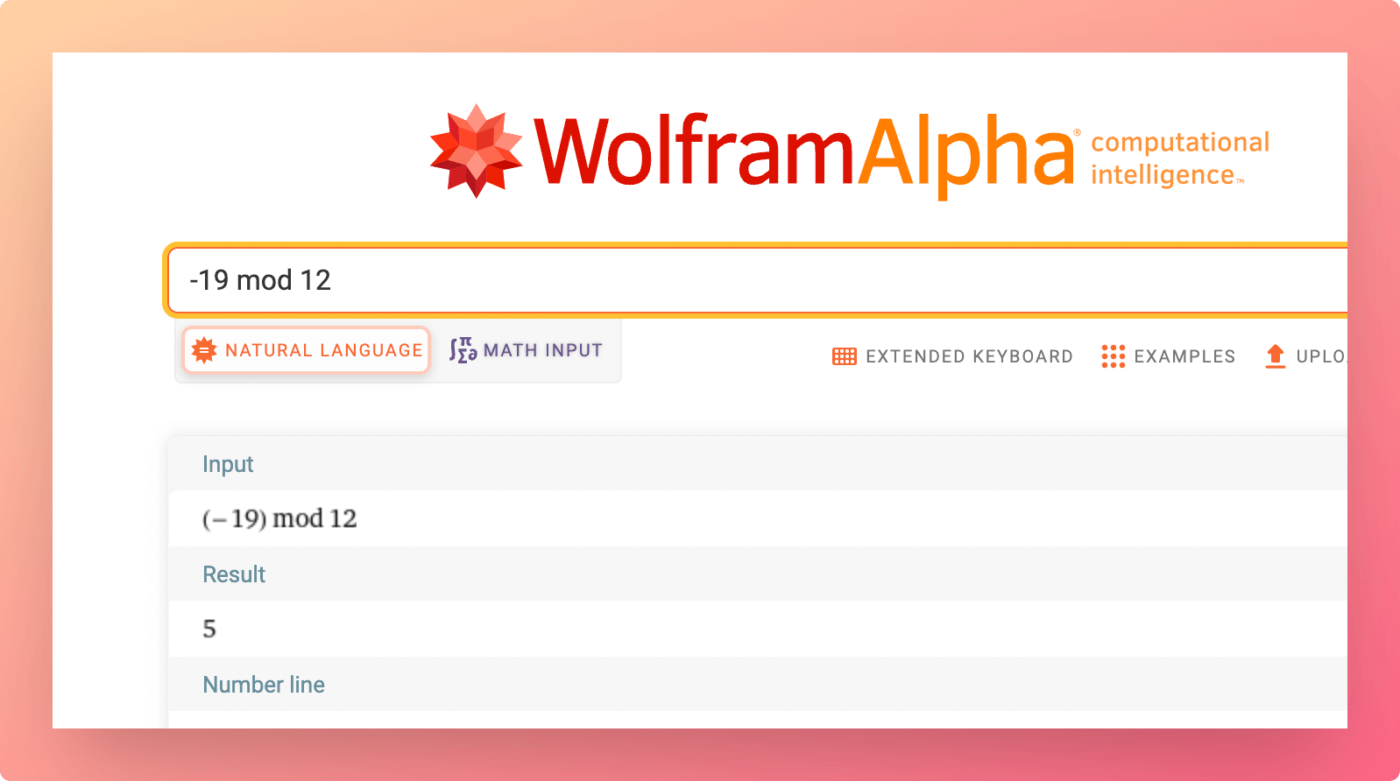
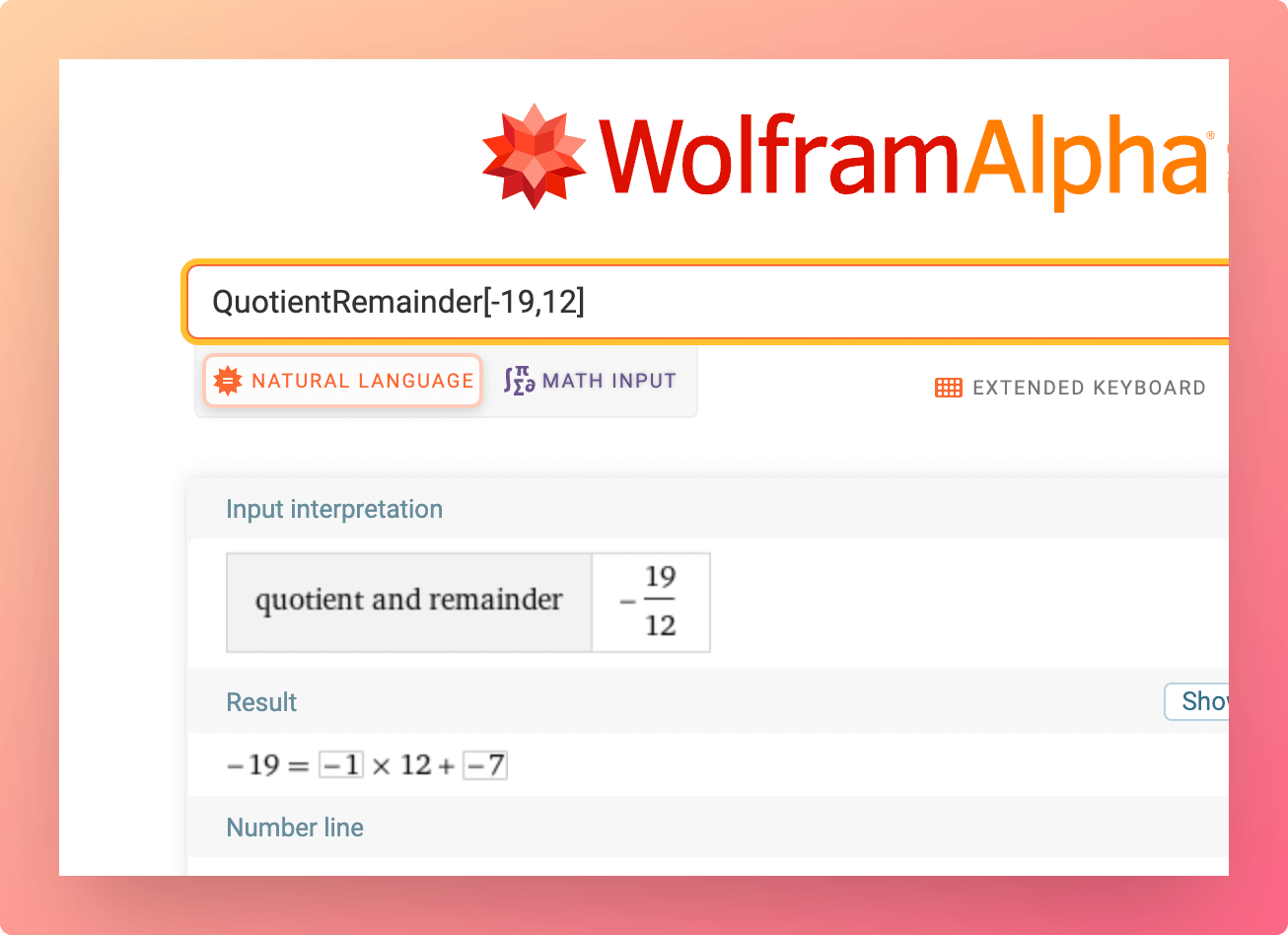
You can prove this using WolframAlpha:

• -19 mod 12 results in 5
• QuotientRemainder[-19,12] results in -7

To calculate a true modulus in Notion, use ((x % y) + y) % y instead:

// Using the % operator
((19 % 12) + 12) % 12

// Using the mod() formula
mod(mod(19, 12) + 12, 12)
Code language: JavaScript (javascript)

// x == dividend, y == divisor
remainder = x - y * Math.trunc(x/y);
Code language: JavaScript (javascript)

Math.trunc(2.9) == 2
Math.trunc(-2.9) == -2
Code language: JavaScript (javascript)

// x == dividend, y == divisor
modulus == x - y * Math.floor(x/y);
Code language: JavaScript (javascript)

Math.trunc(-2.9) == -2
Math.floor(-2.9) == -3
Code language: JavaScript (javascript)

// Remainder function
prop("Dividend") - prop("Divisor") * ((prop("Dividend") / prop("Divisor") >= 0) ? floor(prop("Dividend") / prop("Divisor")) : ceil(prop("Dividend") / prop("Divisor")))

// Modulus function
prop("Dividend") - prop("Divisor") * floor(prop("Dividend") / prop("Divisor"))
Code language: JavaScript (javascript)

Example Database

This example database shows the differing outputs of remainder and true modulus expressions.

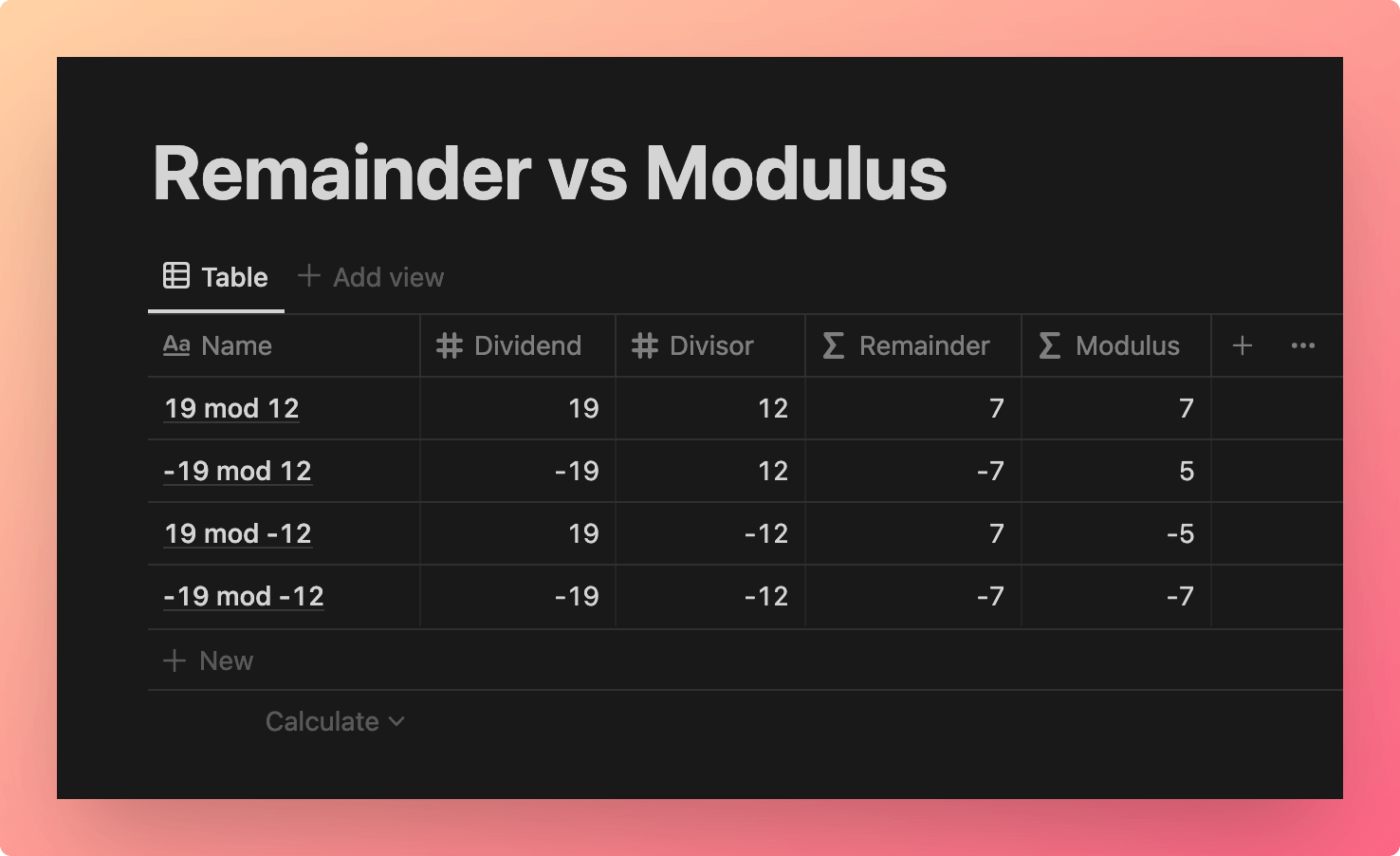
View and Duplicate Database

Notion – The all-in-one workspace for your notes, tasks, wikis, and databases.

A new tool that blends your everyday work apps into one. It’s the all-in-one workspace for you and your team

thomasfrank.notion.site

You can check these results here:

Modulo Calculator

Modulo calculator finds a mod b, the remainder when a is divided by b. The modulo operation returns the remainder in division of 2 positive or negative numbers or decimals.

www.calculatorsoup.com

“Remainder” Property Formula

prop("Dividend") % prop("Divisor")
Code language: JavaScript (javascript)

“Modulus” Property Formula

(prop("Dividend") % prop("Divisor") + prop("Divisor")) % prop("Divisor")
Code language: JavaScript (javascript)

Instead of using hard-coded numbers, I’ve called in each property using the prop() function.