The mathematical constant \(e\) is known as Euler’s Number, and approximately equals 2.718281828459045.
e()
Code language: JavaScript (javascript)In simple terms, the mathematical constant \(e\) is a base value for calculating continuous growth.
\(e\) is used to calculate compound interest, rates of radioactive decay, and many other things.
Many of these types of growth happen continuously. In other words, the growth doesn’t simply happen instantly, at the end of a certain period.
If growth worked that way, then a 100% rate of growth (i.e. a doubling) applied to a value of 1 would result in a total value of 2 at the end of the first period. You’d have no growth at all until the very end, and then… poof! 1 doubles to 2.
But many types of growth – including things like compound interest – happen continuously.
If you have $1 that is earning interest, then the interest it earns can start earning interest itself.
Therefore, by the end of the first period, you won’t have just $2 – you’ll have more. How much more? It depends on how quickly each bit of interest can start earning its own interest.
If it can do it instantly, then you’ll end up with around $2.71 at the end of the first period – in other words, you’ll end up with \(e\).
\(e\) takes a while to fully grok, and my explanation here is purposefully simplified. If you want to learn more about \(e\), check out this guide on BetterExplained:
Example Formula
e() ^ (.3 * 10)
Code language: JavaScript (javascript)Here is an example formula which could be used to model continuous growth of 30% per year over a period of 10 years.
We can express this as \(e^{(rate \ of \ growth \ * \ number \ of \ time \ periods)}\)
Note that we could multiply these exponents without making any change to the output, so e() ^ 3 would work as well.
Good to know: You can also use the exp function to raise \(e\) to a higher power – e.g. e^n is equivalent to exp(n) (where n is a number).
To make this useful, we can multiply it by a starting number. For example:
500 * e() ^ (.3 * 10)
Code language: JavaScript (javascript)This equation would output a final value if we start with 500 and grow it by 30%/year over 10 years. See the answer in the example database below!
Example Database
Using \(e\), we can write a Notion formula that models continuous growth of a starting population by a certain percentage each year over a certain number of years.
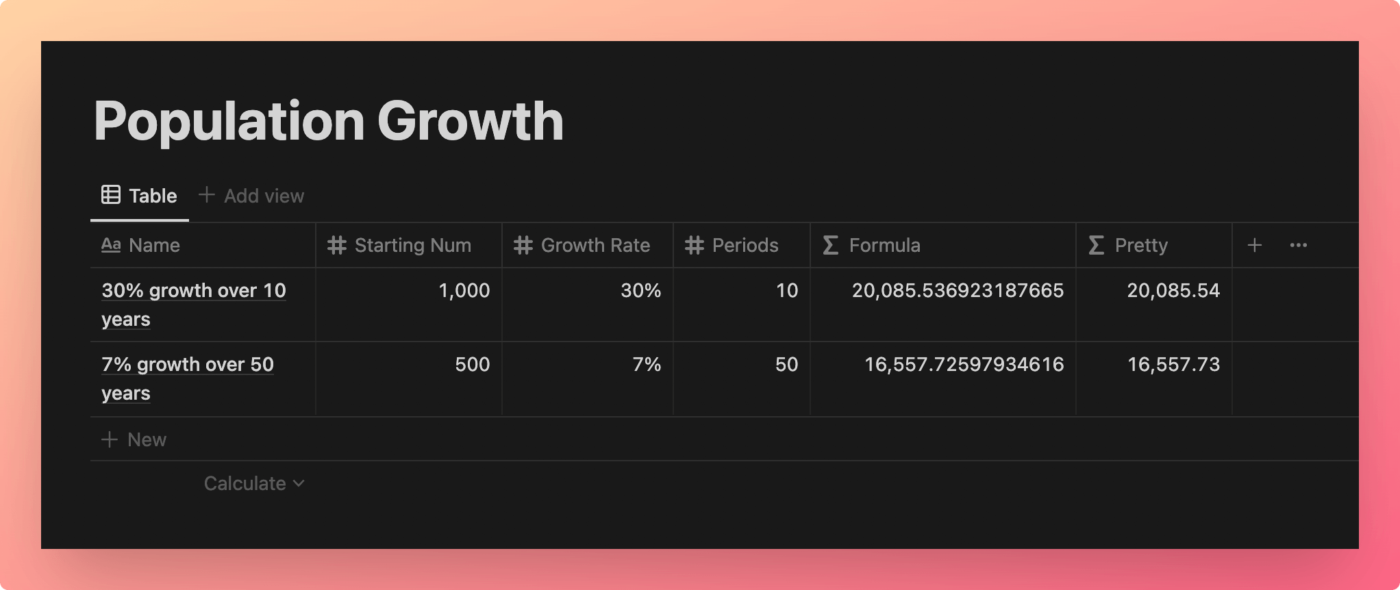
View and Duplicate Database

“Formula” Property Formula
prop("Starting Num") * e() ^ (prop("Growth Rate") * prop("Periods"))
Code language: JavaScript (javascript)Here we’ve just modified the 500 * e() ^ (.3 * 10) example above with variables, which are set by the properties Starting Num, Growth Rate, and Periods.
Note that I’ve also changed the number formatting on Starting Num, Periods, Formula, and Pretty to “Number with commas” in order to make them more readable.
I’ve changed the number formatting on Growth Rate to “Percent”, which actually changes its numeric value. With this formatting, I was able to type 30 in the first row, but Formula interprets it as .30 (the decimal value of 30%).
Other formula components used in this example:


“Pretty” Property Formula
round(prop("Formula") * 100) / 100
Code language: JavaScript (javascript)The Pretty formula simply intakes Formula, then applies the round() function. I use the decimal-place rounding trick to round to two decimal places.
Other formula components used in this example:






