The remainder (%) operator allows you to get the remainder after dividing the first operand with the second operand.
number % number
mod(number, number)
number.mod(number)
Code language: JavaScript (javascript)Notion provides a mod() function as well as the % operator (I’ll just reference % for the rest of this article).
Somewhat confusingly, these do not return a true modulus value; they return a remainder (see: Remainder or Modulus? below).
As % and mod() output a remainder, their output values will take the sign (+/-) of the dividend.
For reference, the dividend is the number being divided by the divisor, which produces the quotient:
\(\frac {dividend}{divisor} = quotient\)Example Formulas
19 % 12 /* Output: 7 */
19 mod 12 /* Output: 7 */
mod(-19, 12) /* Output: -7 */
-19.mod(12) /* Output: -7 */
Code language: JavaScript (javascript)Negative Divisors
If the divisor is negative both mod() and % will now treat it as a negative integer natively.
19 % (-12) /* Output: 7 */
/* prop("negative num") == -12 */
19 % prop("negative num") /* Output: 7 */
19 % -12 /* Output: 7 */
mod(19, -12) /* Output: 7 */
Code language: JavaScript (javascript)Remainder or Modulus?
Just as in JavaScript, Notion’s % operator calculates the remainder of two numbers, not the modulus. Confusingly, the mod() function does this as well, despite its name.
The remainder and modulus of two numbers will be identical when both the dividend and divisor have the same sign (+/-). If their signs differ, however, the modulus will differ from the remainder.
These two articles explain this well:
- Mod and Remainder are Not the Same (Big Machine)
- Remainder operator vs. modulo operator (with JavaScript code) (2Ality)
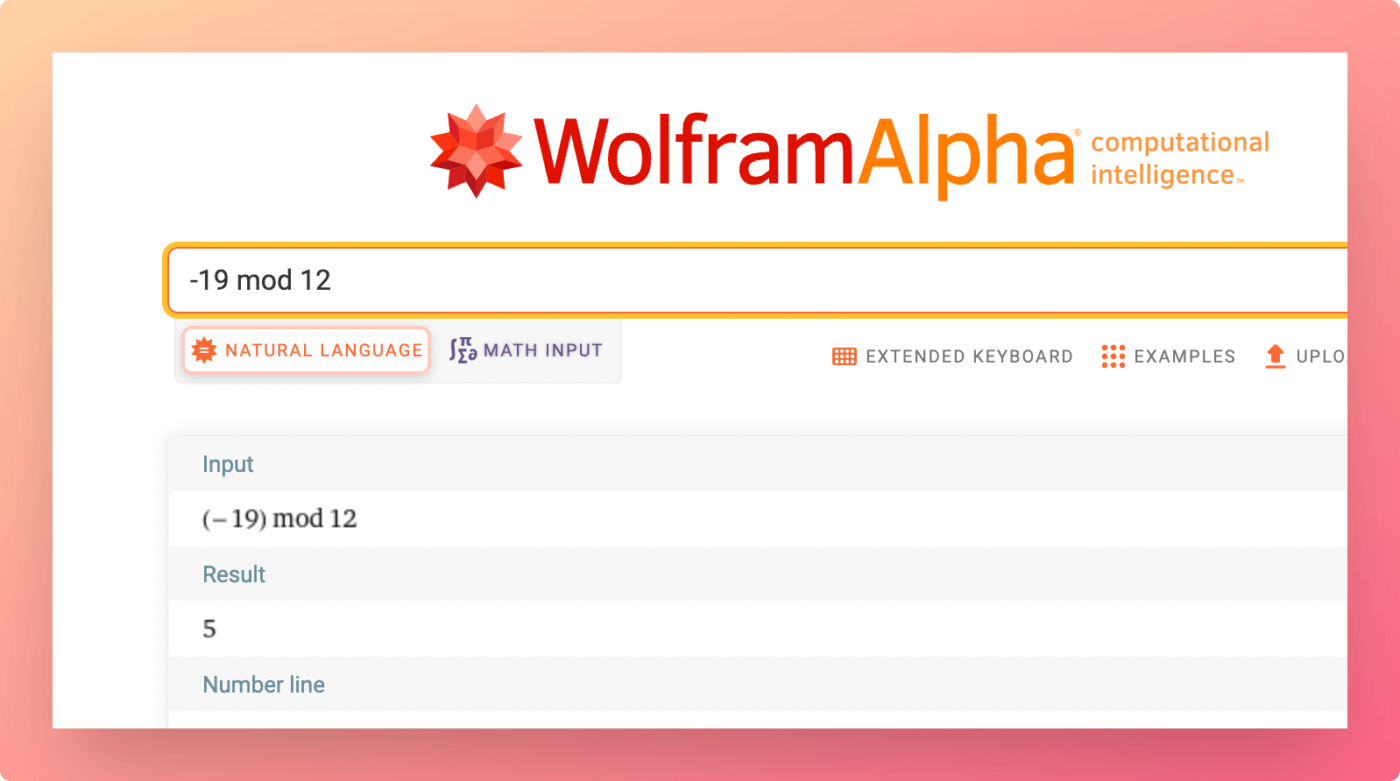
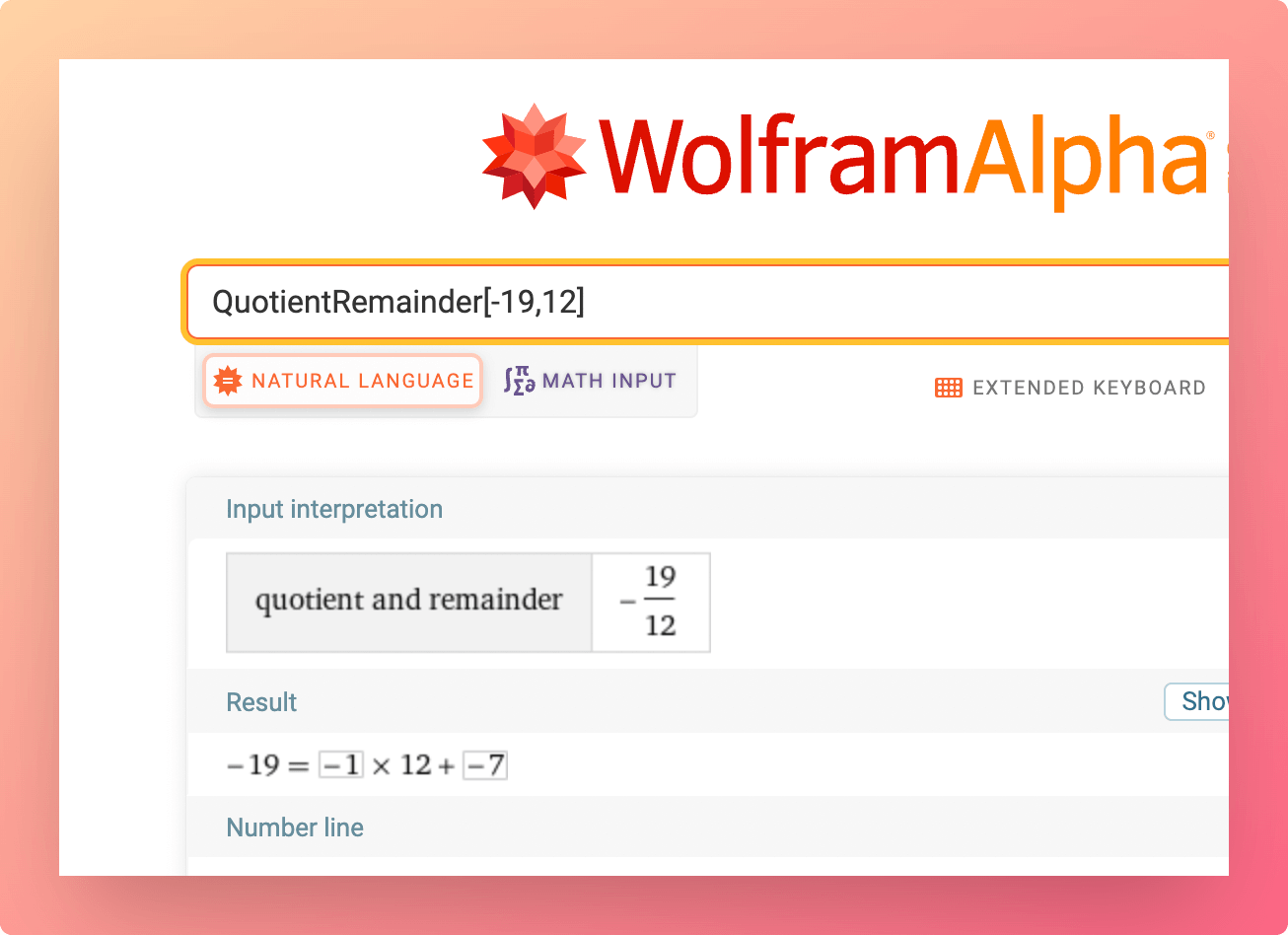
You can prove this using WolframAlpha:
-19 mod 12results in5QuotientRemainder[-19,12]results in-7
To calculate a true modulus in Notion, use ((x % y) + y) % y instead:
// Using the % operator
((19 % 12) + 12) % 12
// Using the mod() formula
mod(mod(19, 12) + 12, 12)
// % operator example using hard-coded negative divisors
((19 % (-12)) + (-12)) % (-12)
Code language: JavaScript (javascript)As noted above in the Negative Divisors section, hard-coded negative divisors in % expressions need to be wrapped in parentheses () so Notion can parse them explicitly as negative integers (see code line 7 in the above code block).
Otherwise, Notion will interpret the - as a unaryMinus operator, rewrite your formula to (x / 100 - y + -y) / 100 - y, and return an incorrect result. However, this isn’t necessary when using the mod() function.
I recommend reading Dr. Axel Rauschmayer’s Remainder Operator vs. Modulo Operator article to fully understand this, but here’s a summary.
To find a remainder, the formula is:
\(remainder = dividend – divisor * quotient\)In JavaScript, the % operator accomplishes this using the following function:
// x == dividend, y == divisor
remainder = x - y * Math.trunc(x/y);
Code language: JavaScript (javascript)The Math.trunc() function simply chops all of the decimals off of a number and returns only what was left of the decimal point. In more precise terms, it rounds a number towards zero, no matter how how the decimal point.
Math.trunc(2.9) == 2
Math.trunc(-2.9) == -2
Code language: JavaScript (javascript)To put it another way, Math.trunc() acts like Math.floor() when its argument is positive, and acts like Math.ceil() when its argument is negative. For reference:
Math.ceil()rounds towards positive infinityMath.floor()rounds towards negative infinity
Note: The trunc() function doesn’t exist in Notion’s formula editor, but you can create it with: (prop("Num") >= 0) ? floor(prop("Num")) : ceil(prop("Num"))
The formula for finding a modulus is the same, with one major difference: it uses the floor() function instead of trunc().
// x == dividend, y == divisor
modulus == x - y * Math.floor(x/y);
Code language: JavaScript (javascript)When the dividend and divisor have the same sign, the results from both formulas will be the same.
But when they are opposite, these formulas return different results.
This happens because trunc() will always return an answer one integer greater than floor() will when both have the same negative integer as their argument.
Math.trunc(-2.9) == -2
Math.floor(-2.9) == -3
Code language: JavaScript (javascript)The difference causes different results in the overall modulus/remainder functions.
For fun, here’s how you could manually create remainder and modulus functions in Notion without using mod(). Note how complicated the remainder code is due to Notion’s lack of a trunc() function!
// Remainder function
prop("Dividend") - prop("Divisor") * ((prop("Dividend") / prop("Divisor") >= 0) ? floor(prop("Dividend") / prop("Divisor")) : ceil(prop("Dividend") / prop("Divisor")))
// Modulus function
prop("Dividend") - prop("Divisor") * floor(prop("Dividend") / prop("Divisor"))
Code language: JavaScript (javascript)Example Database
This example database shows the differing outputs of remainder and true modulus expressions.
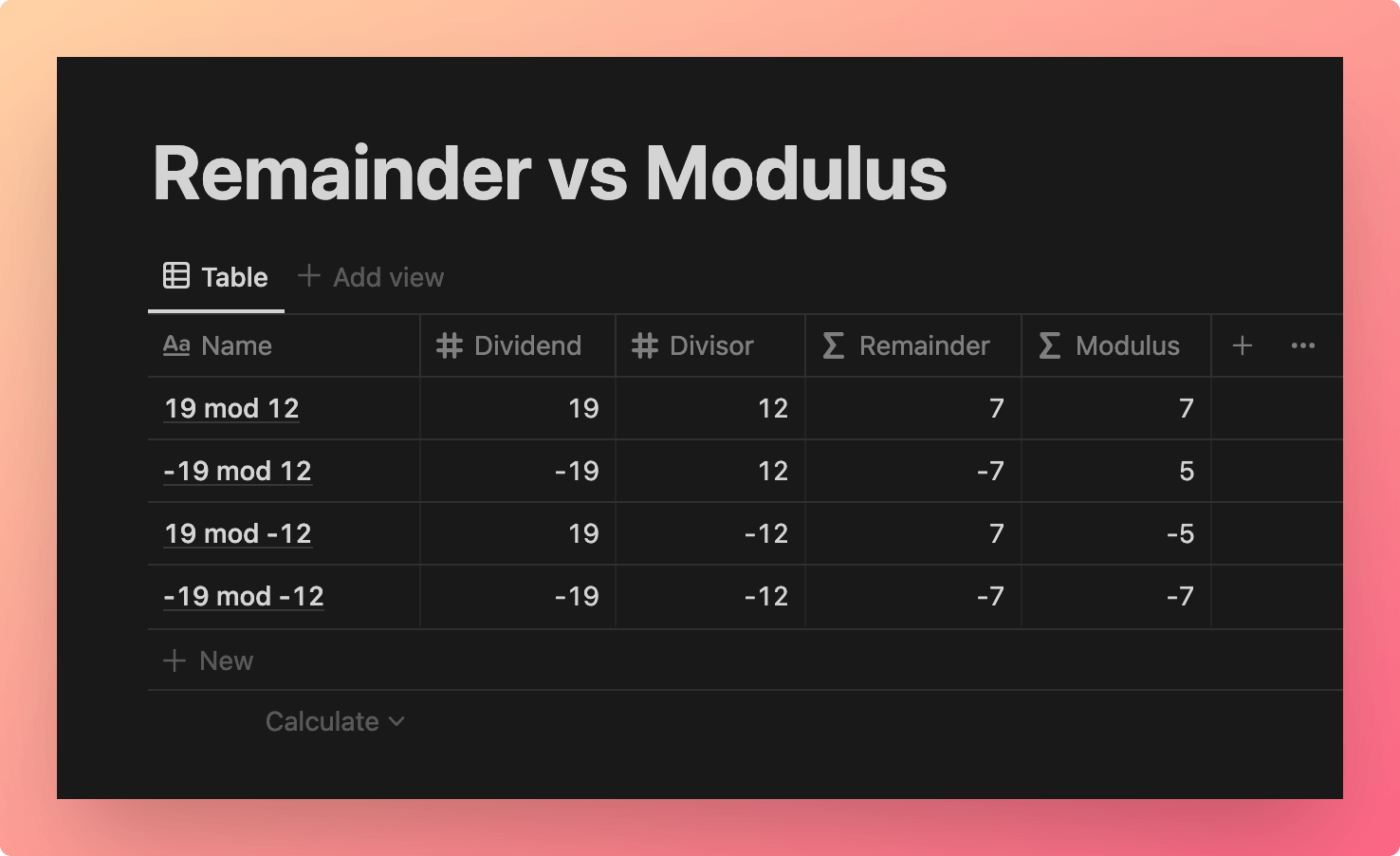
View and Duplicate Database
You can check these results here:
“Remainder” Property Formula
prop("Dividend") % prop("Divisor")
Code language: JavaScript (javascript)“Modulus” Property Formula
(prop("Dividend") % prop("Divisor") + prop("Divisor")) % prop("Divisor")
Code language: JavaScript (javascript)Instead of using hard-coded numbers, I’ve called in each property using the prop() function.